Raspberry Pi 4: Review, Buying Guide, and How to Use

Raspberry Pi is an inexpensive single-board computing device used to power up robots like digital kiosks, smart home devices, and more. Raspberry Pi 4 was launched in 2019 and took the Pi to another level.

It delivers good performance with 4K video output at 60 Hz or power dual monitors as a desktop. The Raspberry Pi 4 came out with 8GB of RAM for serious desktop computing, database hosting, and productivity.

You can buy a Raspberry Pi 4 that belongs to your tech toolkit. The 2GB model of Raspberry Pi 4 starts from just 35 USD. You can use Raspberry Pi 4 as a learning PC for the kids, a web server, a media center, a game emulation machine, the brains of a robot, and an IoT device. It can improve your life and deliver a lot of fun by opening a whole world of possibilities.

In today’s Raspberry Pi 4 Review and Guide topic, I’ll give you the answers to the critical questions required to choose the suitable model of Raspberry Pi 4. If you already own Raspberry Pi 4, then it will help you how to use it.

Should I Buy a Raspberry Pi 4?

First and foremost, should I buy Raspberry Pi 4? Well, it is worth a buy!

Raspberry Pi 4 can run a security camera, play old Arcade games, and do future projects. So, it is worth a buy can buy. But, it isn’t easy to choose the Raspberry Pi model, and you may end buying a different model as per your work or need.

If you’re looking for an all-arounder model for general purposes, then go with the Raspberry Pi 4 B-model. In case you already own an earlier model of Raspberry Pi and are wondering about the features of Raspberry Pi 4, I will guide you on this.

The newer Model has tons of distinctive advantages like two to four times faster speed, USB 3.0 port, true Gigabit Ethernet, and dual video output up to 4K resolution.

Get your Raspberry Pi 4 from here ????

How Does Raspberry Pi 4 Improve on Other Models?

The most significant improvement is the processor of 1.5 GHz Broadcom CPU and GPU with faster RAM. In addition, two USB 3.0 ports allow onboard Ethernet with a true Gigabit connection, dual micro HDMI ports, and support for 4K output. 

The new model supports Gigabit connection with 125 Mbps, whereas the last-gen models support a maximum of 41 Mbps. Two microSD card slot offers faster speed of 50 Mbps theoretically against 25 Mbps on the 3B+.

As the new SoC needs more power, the Raspberry Pi 4 B-model uses a reversible USB Type-C port for charging instead of micro USB Type-B. A power adapter of 3amps and 5volts is required to charge it. Minimum 2.5amps are needed if every peripheral are disconnected.

Which Raspberry Pi 4 Should I Buy?

Currently, three Raspberry Pi 4 models are available in the market. All the models are identical in all terms except the amount of RAM. The entry-level model comes with 2GB of RAM. It is enough for projects like robots, retro arcade machines, etc. It cost 35 USD.

But, if you’re using the Raspberry Pi 4 as a desktop PC, you should get the 4GB model. The 4GB model costs 55 USD. With the Raspbian OS, Raspberry Pi delivers memory-efficient performance. Opening tons of web pages, running lots of apps, and playing games don’t exceed the memory of 4GB RAM.

There is also an 8GB model of Raspberry Pi 4 available. It delivers more utility and advantages over the 4GB model. It cost 75 USD. If you can afford it, then buy an 8GB model for future-proof.

Design and Construction of Rapberry Pi 4

Similar in design and dimensions to its predecessors, Raspberry Pi 4 is powered by a Broadcom BCM2711B0 – the new processor. This new chip is based on a 28nm process. The BCM2711B0 has 1.5 GHz four ARM Cortex-A72 CPU cores, but it’s not quicker than the 1.4 GHz quad-core processor BCM2837B0 in the Raspberry Pi 3 B+ model.

Cortex A72 has a 15-instruction pipeline depth with out-of-order execution. It doesn’t make you wait for the output of one process to start on another. At the same clock speed, Cortex-A72 processors will be faster and more potent than Cortex-A53. The 1GB of DDR2 RAM is also quicker.

And, 8GB of DDR4 RAM in the Pi 4 has increased the bandwidth. More memory is helpful for web surfing. The GPU has also upgraded to VideoCore VI of 500 MHz clock speed. The new architecture allows delivering an output of 4K with a 60Hz frame rate and dual monitors at 4K with a 30 Hz frame rate.

What Ports Does the Raspberry Pi 4 Have?

In terms of ports, the Raspberry Pi 4 provides four USB Type-A connections – two USB 3.0 and two USB 2.0.

✅ A full-size wired connected Gigabit Ethernet port is there.
✅ A 3.5mm audio jack, USB Type-C port for charging
✅ Two micro HDMI ports at the bottom.
✅ On the left side, a micro SD card reader is also present.

On the top, you’ll see ribbon connectors for the Camera Serial Interface (CSI) and Display Serial Interface (DSI). It provides a dedicated Camera connection as a PC webcam, Motion-alert security camera to Raspberry Pi 4.

You can also connect a camera to a USB port. Micro HDMI ports are there to deliver output to a screen. Moreover, the set of GPIO pins can connect motors, lights, sensors, and a huge HAT ecosystem of HATs.

What Kind of Power Adapter and USB Type-C cables Do I Need for Raspberry Pi 4?

To power up your Raspberry Pi 4, you will need a power adapter of at least 3 amps and 5 volts with a USB Type-C wire. You can also power the Pi 4 with a Mobile charger and a USB PD power bank of USB Type-C.

Seeing the lightning bolt icon at the top, you can understand whether the board is operating at reduced power or not. Similar to other models, the Raspberry Pi 4 also has no power switch. To turn it on, plug in directly and shut down the OS first, and then unplug the cable.

Theoretically, any USB Type-C to Type-C cable should work. But, E-marked USB cables are usually used. These cables offer high-speed data transfer up to 3Gbps over a USB 3.0 port.

How Do I Get Started with Raspberry Pi 4?

You need to put a blank micro SD card into your PC or Mac. After that, use Raspberry Pi Imager to ‘burn’ a disk image of Raspberry Pi OS on the micro SD card. Then, put the microSD card into the Raspberry Pi and turn it on.

Now, follow the setup process shown in Raspberry Pi OS. However, you can easily overclock the 1.5 GHz CPU up to 2 GHz. GPU frequency can also be increased from 500MHz to 600MHz.

Storage on Raspberry Pi 4: How to make it faster

Besides the fast processor, RAM and GPU, your storage also need to be fast. Otherwise, everyday tasks such as opening apps and files will lag.

Similar to previous models of Raspberry Pi, the Raspberry Pi 4 B-model has a micro SD card reader as a primary storage device. But, this time, it is constrained and has a top transfer rate of 50 Mbps. There is an unknown limit on capacity.

However, the Raspberry Pi 4 B-model card is rated for 100 Mbps read and 60 Mbps write. But it delivers 45.7 Mbps read and 27.7 Mbps write.

You will get better speed and storage performance by using an external SSD or a quick USB Flash drive. The Raspberry Pi 4 B-model is the first Pi with USB 3.0 ports.

Theoretically, it has a bandwidth of 625 Mbps. Using a Western Digital Blue SSD in a USB to M.2 enclosure increases its transfer rates up to 2 to 13 times faster. It also opens the applications faster. But, using a regular USB Flash drive is slower than using a microSD card.

With the recent firmware update, you can take out a micro SD card and correct all the files to an external drive like SSD and USB Flash drive.

What Kind of Wi-Fi and Networking Does Raspberry Pi 4 Have?

Similar to its predecessors, the Raspberry Pi 4 B-model has the same 802.11ac Wi-Fi running on 2.4GHz or 5GHz bands. But, it improves over Bluetooth and supports Bluetooth 5.0.

And, the Ethernet port also increases its bandwidth to offer a full gigabit connection. The Raspberry Pi 4 B-model has achieved 943 Mbps Ethernet connection speed, i.e., five times of Pi 3 B+ model.

GPIO Pins on Raspberry Pi 4: What’s the Pinout?

The Raspberry Pi 4 B-model has a set of 40 GPIO (General Input / Output) pins. The pin count and layout remain the same as previous models. So that any sensors, LED screen, and HATs (Hardware Attached on Top) can be added.

The GPIO pins support additional connections for the hardcore makers, i.e., SPI, I2C, and UART connections. A new GPIO pinout is added to the Pi 4 with capabilities.

Using the Raspberry Pi 4 as PC: Is it Good Enough?

The capability of using a like PC is one of the biggest highlights of the Raspberry Pi 4. You can do light work, web surfing, and playing basic games. Dual monitors output is desirable.

Based on daily work of writing, editing and researching, it doesn’t make any problem. Without 4GB of RAM, it can switch into 15 different opened tabs smoothly. Even it works well with 60 opened tabs, several programming, and running productivity apps. The use of SSD instead of a micro SD card also makes the performance faster.

The free GIMP software allows for editing still images in a decent way. LibreOffice helps to crunch spreadsheets and compose documents outside of Google Docs.

4K Output, Video Streaming on Raspberry Pi 4

The Raspberry Pi 4 boasts dual micro HDMI ports. You can connect separate TV or monitor to each port. Both of them will support a 4K resolution.

You can operate multiple 4K displays at a 30Hz refresh rate. Whereas, single 4K and 1080p display can be operated at a 60Hz refresh rate. 4K at 30Hz is tolerable, whereas 60Hz is better during 4K. But it needed extra voltage that causes the heat of the CPU.

Web surfing to look still images and 4K video streaming is great in Raspberry Pi 4 B-model. Raspberry Pi 4 isn’t optimized for the VP9 compression that YouTube uses. So, jerky videos will appear on full screen. Also, paid streaming sites won’t run due to DRM protection.

Follow the instructions of Ventz. It is a special developer version of Chromium that allows running streaming services seamlessly. Moreover, launch the Raspberry Pi configuration tool and change the GPU memory to 256 to adjust the amount of video memory.

Retro Gaming on the Raspberry Pi 4

Raspberry Pi is famous for Game emulation. Although officially RetroPie didn’t support Raspberry Pi 4, Pi 4 owners can choose either RetroPie or Lakka through the interface and broad support.

You can play a wide variety of games like classic, arcade, and many more by using an emulator. The Raspberry Pi 4’s faster processor delivers better-emulating performance for demanding games like Sega Genesis and Nintendo 64 (N64), and the N64 title GoldenEye 007.

Using Raspberry Pi 4 as a Web Server: Easy and Fast

Set up as a web server of a Raspberry Pi is one of the most popular use. The Raspberry Pi 4 can handle 3,983 requests per second, according to the Phoronix Apache Test. Pi 4 has 40% improved their web server capabilities to deliver heavier web pages.

Including, they can serve more visitors at the same time without lag. Many web applications use the PHP server for fast processing. The side scripting language of PHP can help a lot. According to PHPBench, the Raspberry Pi 4 B-model scored 101,540.

Now, let’s look at the previous models of Raspberry Pi models and follow the series up to the latest model.

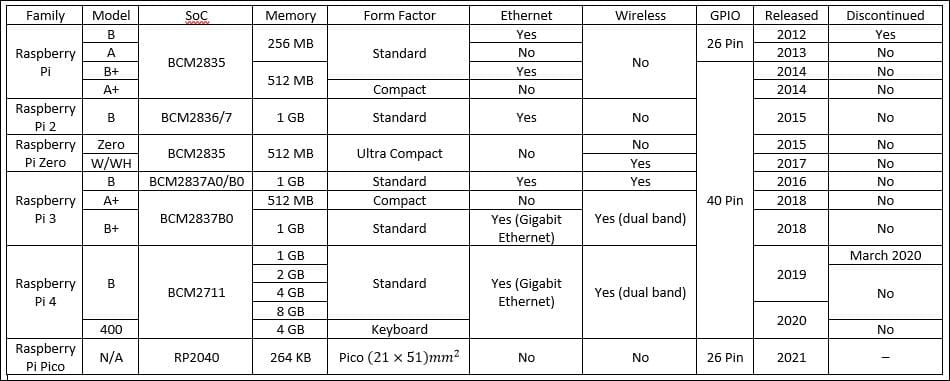
Background of Raspberry Pi and Latest Models

Three series of Raspberry Pi, along with several generations of each series, have been released. Raspberry Pi is a small single-board computer (SBCs). It features a Broadcom system, integrated with an ARM-compatible Central Processing Unit (CPU) on a chip (SoC) and on-chip graphics processing unit (GPU).

The basic Raspberry Pi model comes into use to teach computer science in schools and in developing countries. The original product is tailor-made for use in robotics, weather monitoring, the adoption of HDMI and USB devices by computer and electronic hobbyists.

The Raspberry Pi Pico model has an RP2040 system integrated with an ARM-compatible Central Processing Unit (CPU) on-chip. Let’s discuss the models of Raspberry Pi from their starting generations to the latest ones.

1) Raspberry Pi B-Model and A-Model

Raspberry Pi B-model is the first generation of Raspberry Pi released in February 2012. Following this, Model A is simpler and cheaper. The A+ models cost 25 USD whereas the B+ model costs 35 USD.

2) Raspberry Pi B+ Model and A+ Model

A year later, in 2014, Raspberry Pi has launched an improved compute module design B+ model and A+ model. These embedded applications feature credit-card-sized ARM11 processors, which represent the standard mainline form-factor. It A+ model costs 20 USD and the B+ model costs 25 USD approximately.

3) Raspberry Pi 2

In 2015, the Raspberry Pi 2 was released. Initially, it comes with a 32-bit quad-core ARM Cortex-A7 processor of 900 MHz clock speed and 1 GB RAM. But, it has upgraded to the 64-bit quad-core ARM Cortex-A53 processor with the same clock speed. It costs 35 USD.

4) Raspberry Pi Zero

A Raspberry Pi Zero is small and has smaller capabilities of reduced input/output (I/O) and general-purpose input/output (GPIO). It was released in November 2015. It costs 5 USD.

5) Raspberry Pi 3 B-Model

In February 2016, Raspberry Pi 3 B-Model was released. It is powered by a 1.2 GHz 64-bit quad-core ARM Cortex-A53 processor. It also features 802.11n Wi-Fi, USB boot, and Bluetooth capabilities.

6) Raspberry Pi Zero W and WH

Previously launched Raspberry Pi Zero upgraded with Wi-Fi and Bluetooth capabilities and launched with the new name Raspberry Pi Zero W on 28 February 2017. It costs 10 USD.

And, the new Model Raspberry Pi Zero WH has launched with pre-soldered general-purpose input/output (GPIO) headers on 12 January 2018. It costs 17 USD.

7) Raspberry Pi 3 B+ Model

On Pi Day 2018, the Raspberry Pi 3 B+ Model got launched. It has a faster 1.4 GHz processor, 2.4GHz to 5GHz dual-band 802.11ac Wi-Fi (100 Mbit/s), and also three-times faster gigabit Ethernet with an internal USB 2.0 connection of 300 Mbit/s speed. The other features are power over Ethernet with the add-on PoE HAT, network boot, and USB boot (it doesn’t require an SD card anymore). It costs 35 USD.

8) Raspberry Pi 4 B-Model

Raspberry Pi 4 B-Model was released in June 2019. It is powered by a 1.5 GHz 64-bit quad-core ARM Cortex-A72 processor. It comes with onboard 802.11ac Wi-Fi, full gigabit Ethernet, Bluetooth 5.0, two USB 3.0 ports, two USB 2.0 ports, dual-monitor (up to 4K resolution) via a pair of micro HDMI Type-D ports, and 2-8 GB of RAM.

Initially, the Raspberry Pi 4 had a flawless design fixed in the late release of 2019. The Raspberry Pi 4 B-model is also powered via a USB Type-C port with an appropriate PSU to enable additional power to downstream peripherals.

For 2GB model of Raspberry Pi 4, it costs 35 USD. For 4GB of model it costs 55 USD, and 8GB of models costs 75 USD.

9) Raspberry Pi 400

In November 2020, Raspberry Pi 400 was released with a derived custom board of the existing Raspberry Pi 4. It is especially remodeled with an attached keyboard with 4 GB of LPDDR4 RAM. A robust cooling solution increases the clock speed up to 1.8 GHz of the Raspberry Pi 400’s Broadcom BCM2711C0 processor. It is slightly higher than the Raspberry Pi 4.

1) Raspberry Pi Pico

The latest Raspberry Pi Pico was released in January 2021. It has a retail price of 4 USD. It was the first board of Raspberry Pi integrated with a single microcontroller chip RP2040. It is designed in the UK. The Raspberry Pi Pico-model has 264 KB of RAM and 2 MB of flash memory.

It is programmable in C, Circuit Python, and Micro Python. To build accessories of Raspberry Pi Pico and other boards, it uses an RP2040 silicon platform. It has partnered with Arduino, SparkFun, Vilros, Pimoroni, and Adafruit.

Last words on Raspberry Pi 4

The Raspberry Pi 4 is the best single-board computer. It is powerful enough to be used as a desktop computer in a pinch. But, many users don’t switch their computers. The most significant benefit of the Raspberry Pi 4 is its performance.

The innovators harness the power to create new IoT devices, robots, and servers.
That’s all for now. Hope you like today’s article on Raspberry Pi 4 review and gain some knowledge about its use. Share it among your friends who don’t know about

Raspberry Pi or are confused about choosing the suitable model of Raspberry Pi.
Moreover, if you have more information about Raspberry Pi 4, share it with us in the comment section. Also, let us know your experience in the comment with Raspberry Pi 4 or any other model you have. I will come back with another topic soon.

FAQs on Raspberry Pi 4